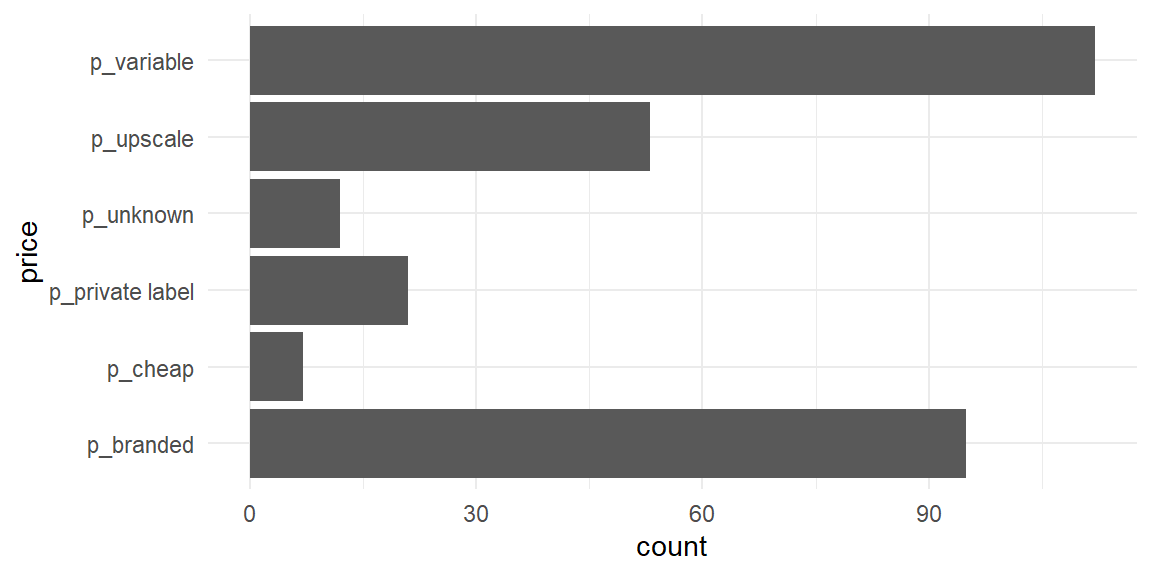Rows: 300
Columns: 36
$ breakfast <fct> breakfast, breakfast, Not.breakfast, Not.breakfast, b…
$ tea.time <fct> Not.tea time, Not.tea time, tea time, Not.tea time, N…
$ evening <fct> Not.evening, Not.evening, evening, Not.evening, eveni…
$ lunch <fct> Not.lunch, Not.lunch, Not.lunch, Not.lunch, Not.lunch…
$ dinner <fct> Not.dinner, Not.dinner, dinner, dinner, Not.dinner, d…
$ always <fct> Not.always, Not.always, Not.always, Not.always, alway…
$ home <fct> home, home, home, home, home, home, home, home, home,…
$ work <fct> Not.work, Not.work, work, Not.work, Not.work, Not.wor…
$ tearoom <fct> Not.tearoom, Not.tearoom, Not.tearoom, Not.tearoom, N…
$ friends <fct> Not.friends, Not.friends, friends, Not.friends, Not.f…
$ resto <fct> Not.resto, Not.resto, resto, Not.resto, Not.resto, No…
$ pub <fct> Not.pub, Not.pub, Not.pub, Not.pub, Not.pub, Not.pub,…
$ Tea <fct> black, black, Earl Grey, Earl Grey, Earl Grey, Earl G…
$ How <fct> alone, milk, alone, alone, alone, alone, alone, milk,…
$ sugar <fct> sugar, No.sugar, No.sugar, sugar, No.sugar, No.sugar,…
$ how <fct> tea bag, tea bag, tea bag, tea bag, tea bag, tea bag,…
$ where <fct> chain store, chain store, chain store, chain store, c…
$ price <fct> p_unknown, p_variable, p_variable, p_variable, p_vari…
$ age <int> 39, 45, 47, 23, 48, 21, 37, 36, 40, 37, 32, 31, 56, 6…
$ sex <fct> M, F, F, M, M, M, M, F, M, M, M, M, M, M, M, M, M, F,…
$ SPC <fct> middle, middle, other worker, student, employee, stud…
$ Sport <fct> sportsman, sportsman, sportsman, Not.sportsman, sport…
$ age_Q <fct> 35-44, 45-59, 45-59, 15-24, 45-59, 15-24, 35-44, 35-4…
$ frequency <fct> 1/day, 1/day, +2/day, 1/day, +2/day, 1/day, 3 to 6/we…
$ escape.exoticism <fct> Not.escape-exoticism, escape-exoticism, Not.escape-ex…
$ spirituality <fct> Not.spirituality, Not.spirituality, Not.spirituality,…
$ healthy <fct> healthy, healthy, healthy, healthy, Not.healthy, heal…
$ diuretic <fct> Not.diuretic, diuretic, diuretic, Not.diuretic, diure…
$ friendliness <fct> Not.friendliness, Not.friendliness, friendliness, Not…
$ iron.absorption <fct> Not.iron absorption, Not.iron absorption, Not.iron ab…
$ feminine <fct> Not.feminine, Not.feminine, Not.feminine, Not.feminin…
$ sophisticated <fct> Not.sophisticated, Not.sophisticated, Not.sophisticat…
$ slimming <fct> No.slimming, No.slimming, No.slimming, No.slimming, N…
$ exciting <fct> No.exciting, exciting, No.exciting, No.exciting, No.e…
$ relaxing <fct> No.relaxing, No.relaxing, relaxing, relaxing, relaxin…
$ effect.on.health <fct> No.effect on health, No.effect on health, No.effect o…Chapter 2:
Exploratory Data Analysis (EDA)
Two modes of data analysis
Hypothesis-generating
- “Exploratory analysis”
- Aim is to explore data to discover new patterns
- Results must not be presented as formal tests of a priori hypotheses
- Testing a hypothesis using the same data that gave rise to the hypothesis is circular reasoning
Hypothesis-testing
- “Confirmatory analysis”
- Aim is to evaluate evidence for specific a priori hypotheses
- The hypotheses and ideas were conceived of before the data were observed
- Can be used for formal scientific inference
Presenting hypothesis-generating analyses as hypothesis-testing analyses (i.e., pretending the hypotheses were conceived prior to the analysis) is scientifically dishonest, and a major contributor to the replication crisis in science.
Plots for categorical data
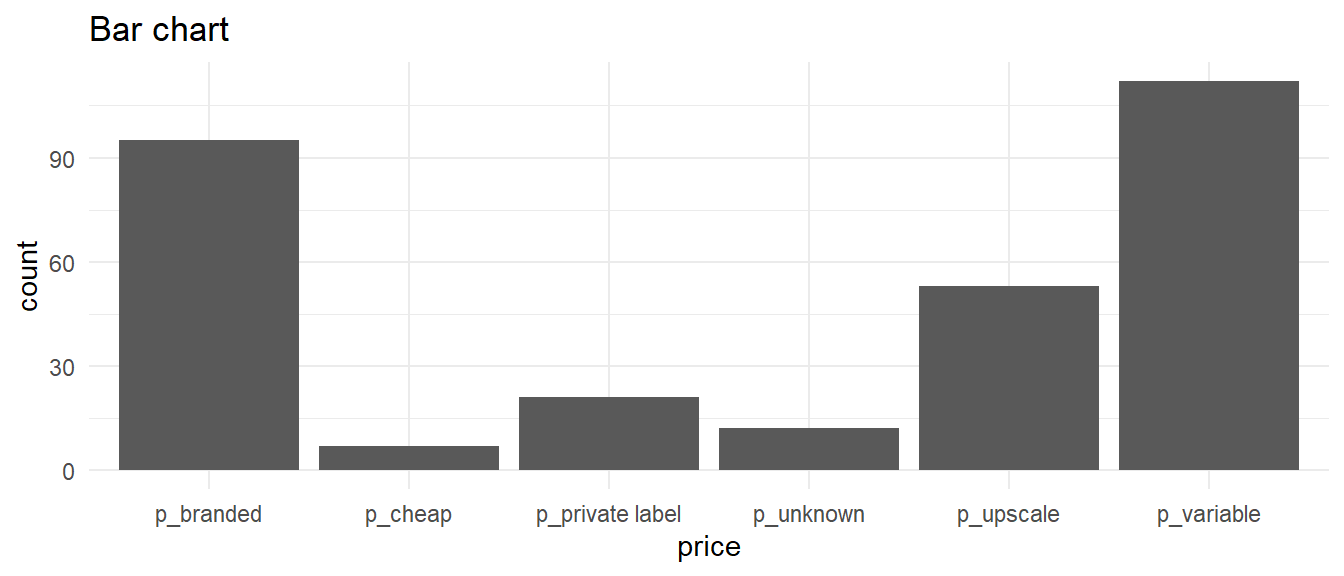
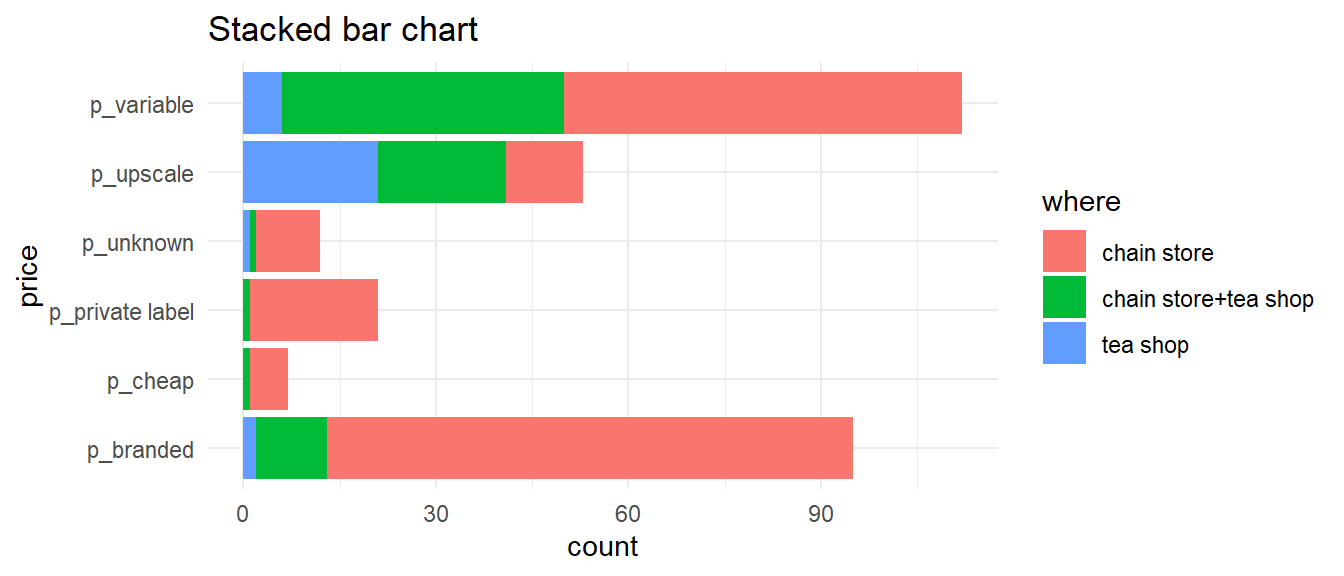
Bar graphs
- Show the frequency of each category (level) in categorical variables
- The height of each bar is proportional to the frequency
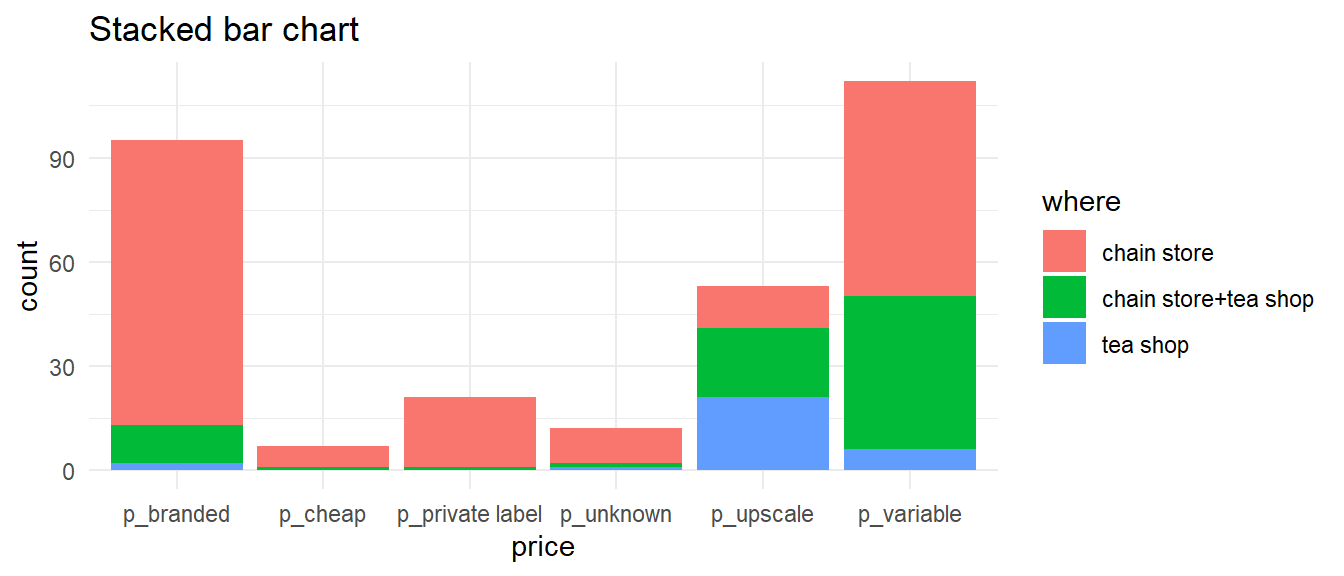
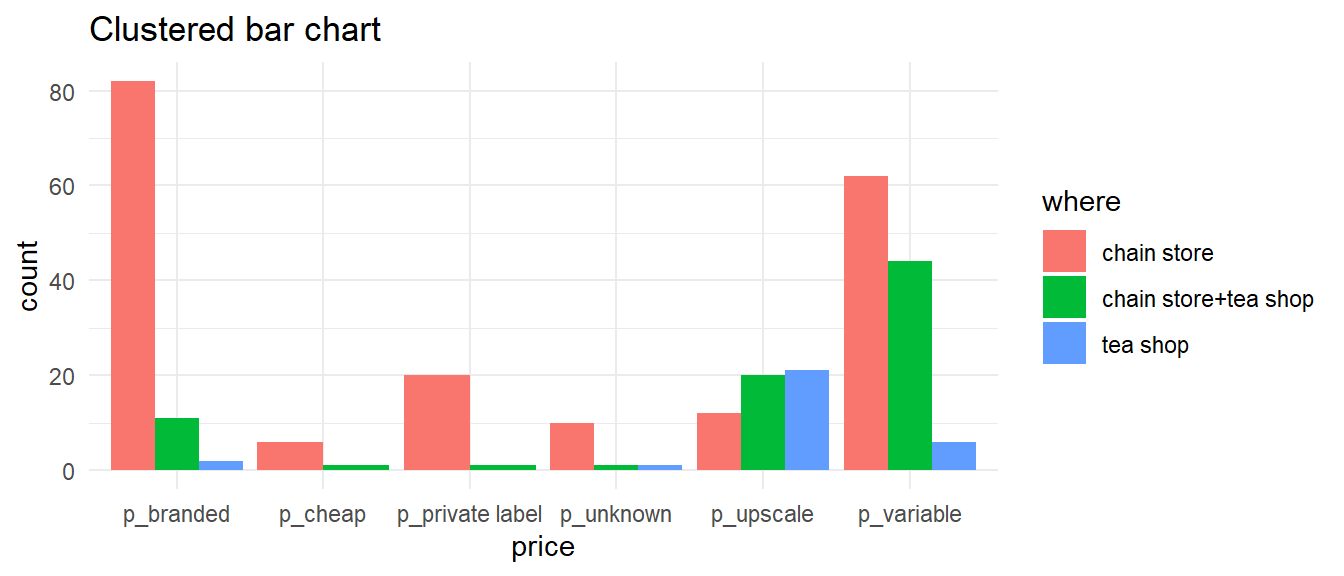
- Can be “stacked” or “clustered”
Tea data
Data from 300 individuals’ tea-drinking habits (18 questions), perceptions (12 questions), and personal details (4 questions).
Bar charts — one variable
Bar charts — two variables
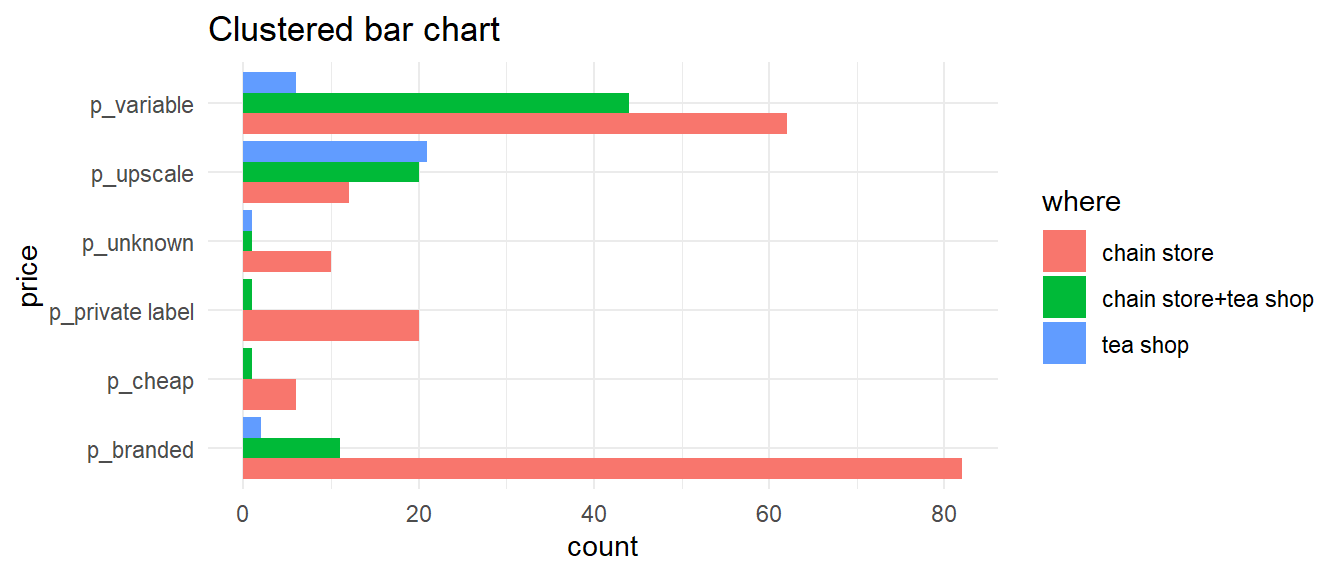
Bar charts - flipped
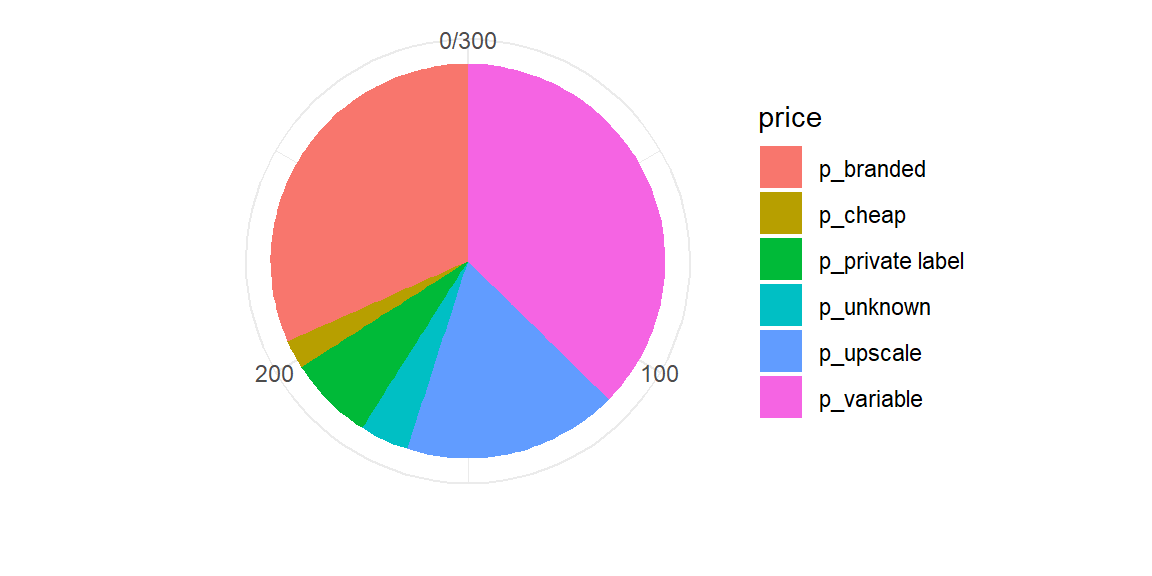
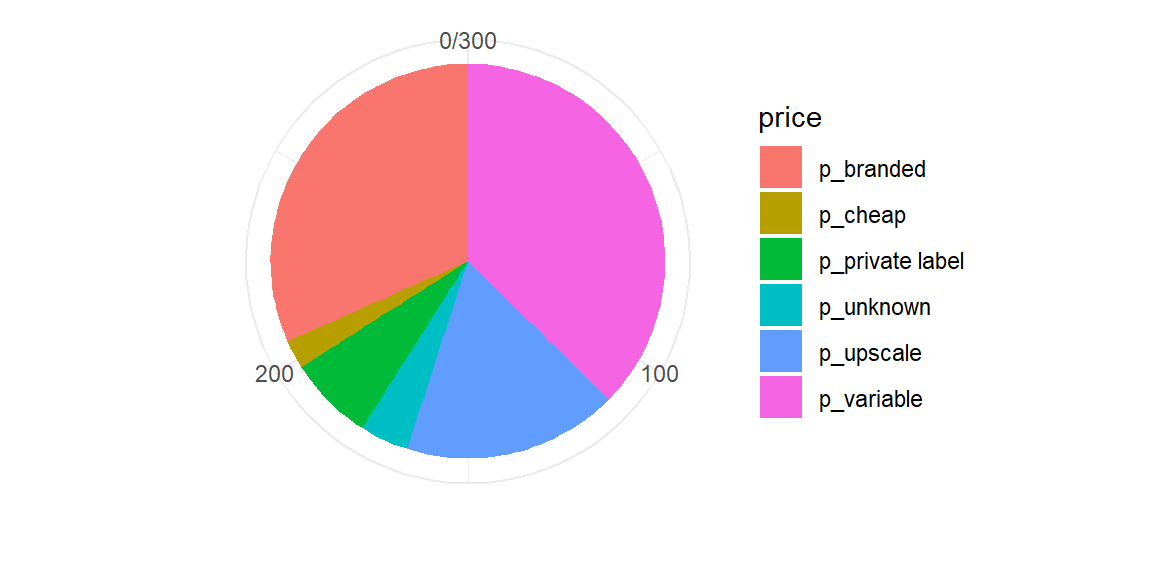
Pie charts (yeah nah)
Pie charts (yeah nah)
- Pie charts are popular but not usually the best way to show proportional data
- Requires comparison of angles or areas of different shapes
- Bar charts are almost always better
https://shiny.massey.ac.nz/anhsmith/demos/explore.counts.of.factors/
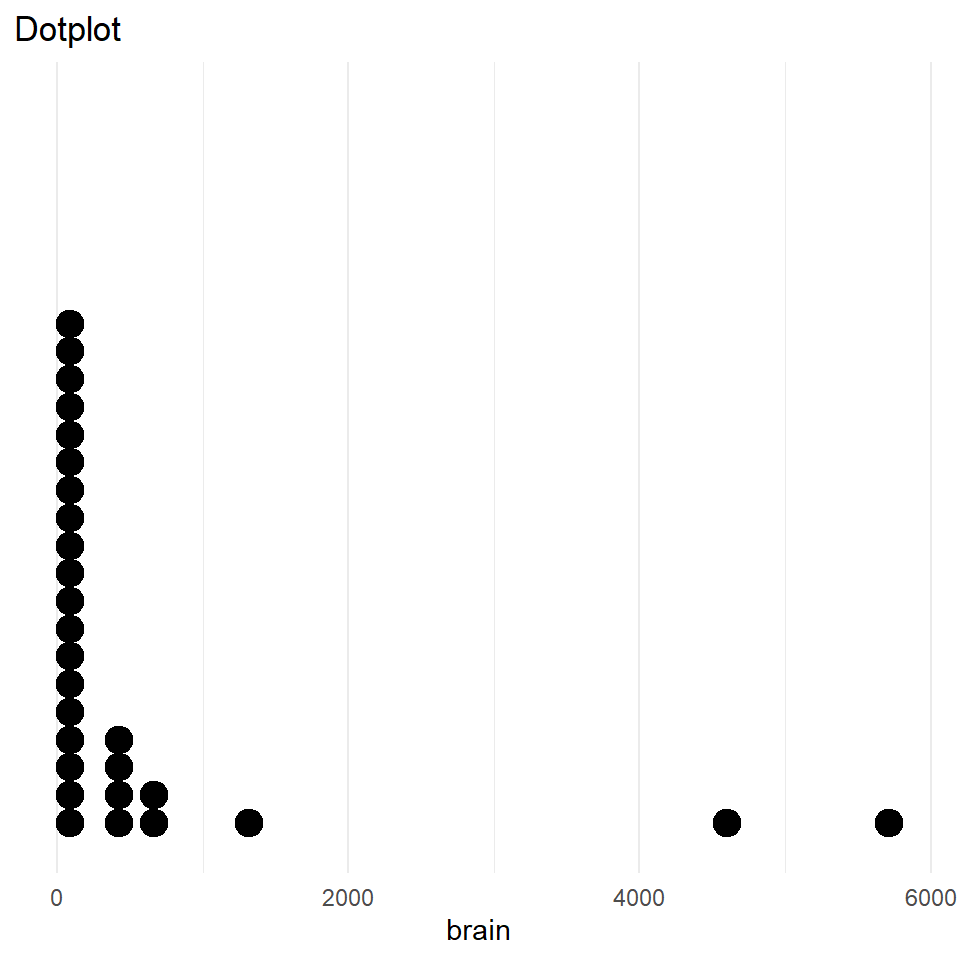
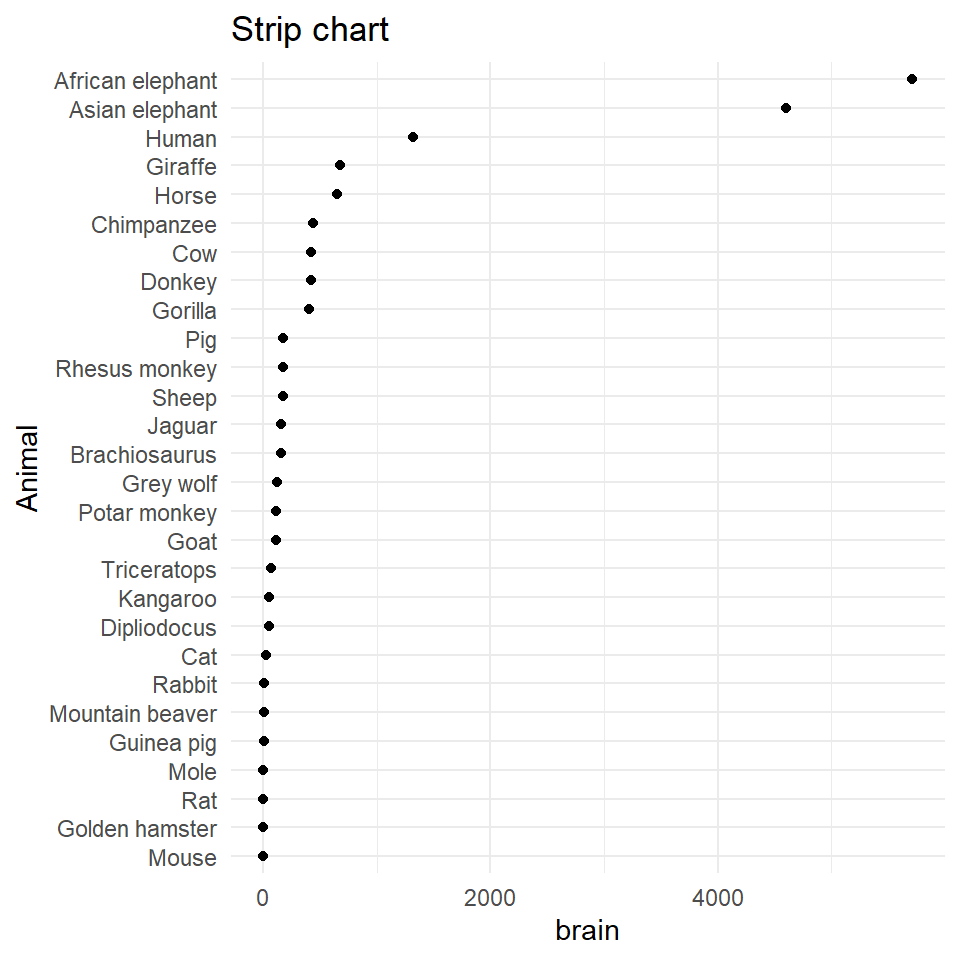
One-dimensional graphs
Dotplots and strip charts display one-dimensional data (grouped/ungrouped) and are useful to discover gaps and outliers.
Often used to display experimental design data; not great for very small datasets (<20)
One-dimensional graphs
Dotplots and strip charts display one-dimensional data (grouped/ungrouped) and are useful to discover gaps and outliers.
Often used to display experimental design data; not great for very small datasets (<20)
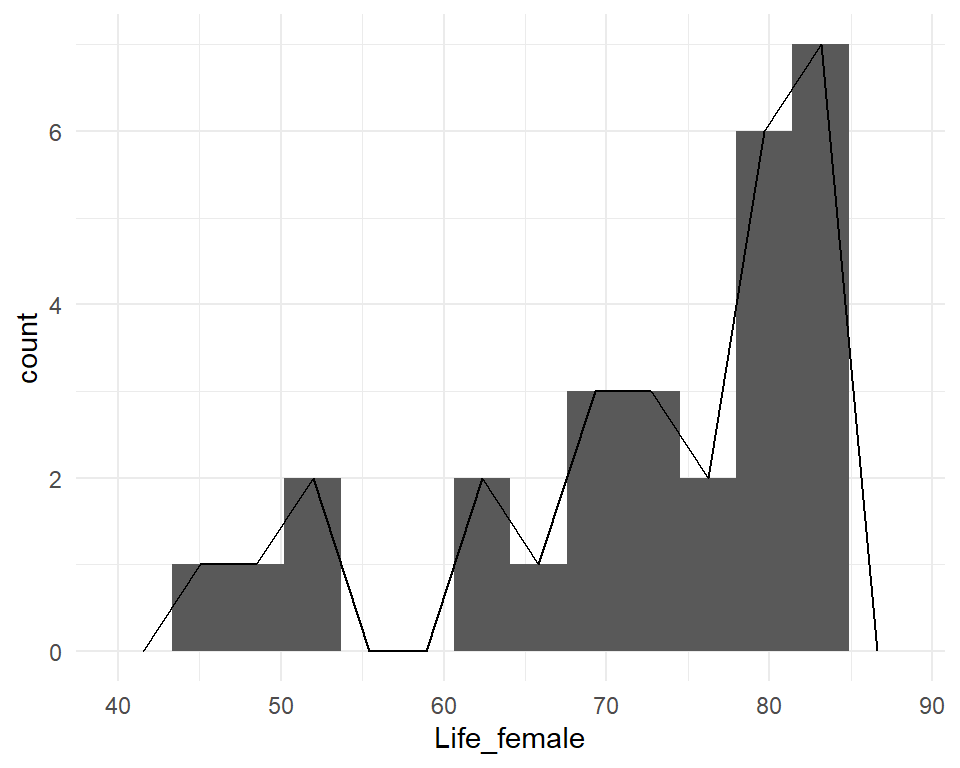
Histograms
Divide the data range into “bins”, count the occurrences in each bin, and make a bar chart.
Y-axis can show raw counts, relative frequencies, or densities
set.seed(1234); dfm <- data.frame(X = rnorm(50, 100))
p1 <- ggplot(dfm, aes(X)) + geom_histogram(bins = 20) + ylab("count") + ggtitle("Frequency histogram", "Heights of the bars sum to n")
p2 <- ggplot(dfm) + aes(x = X, y = after_stat(count/sum(count))) + geom_histogram(bins = 20) + ylab("relative frequency") +
ggtitle("Relative frequency histogram", "Heights sum to 1")
p3 <- ggplot(dfm) + aes(x = X, y = after_stat(density)) + geom_histogram(bins = 20) +
ggtitle("Density histogram","Heights x widths sum to 1")
library(patchwork); p1+p2+p3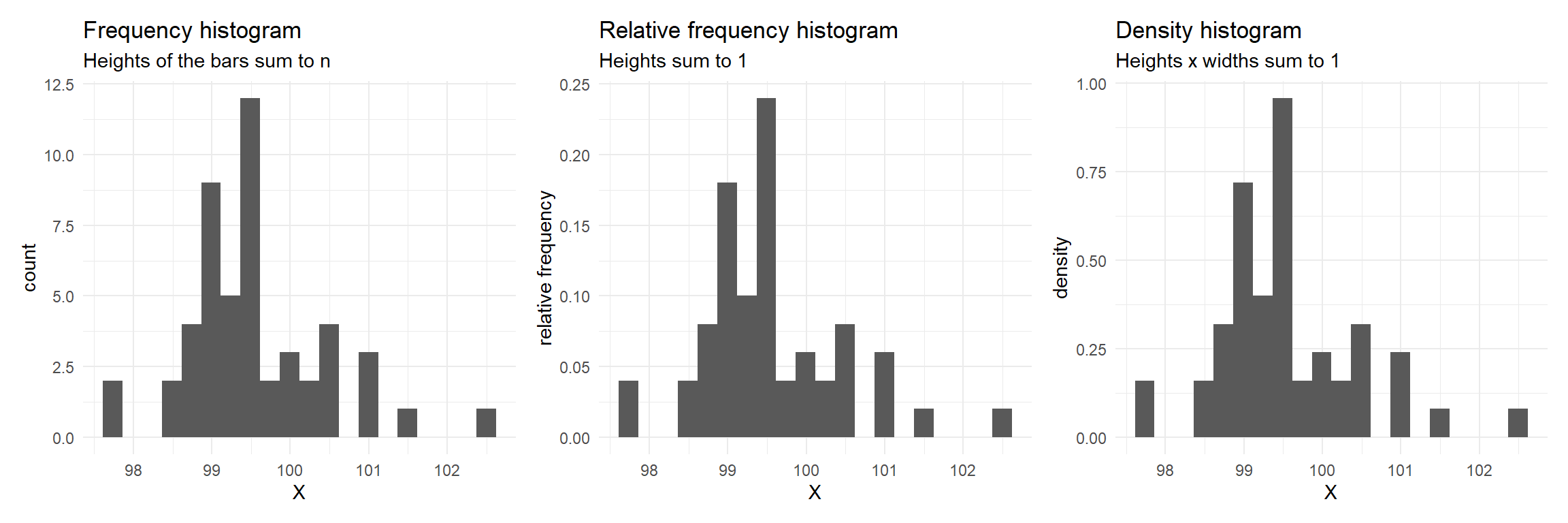
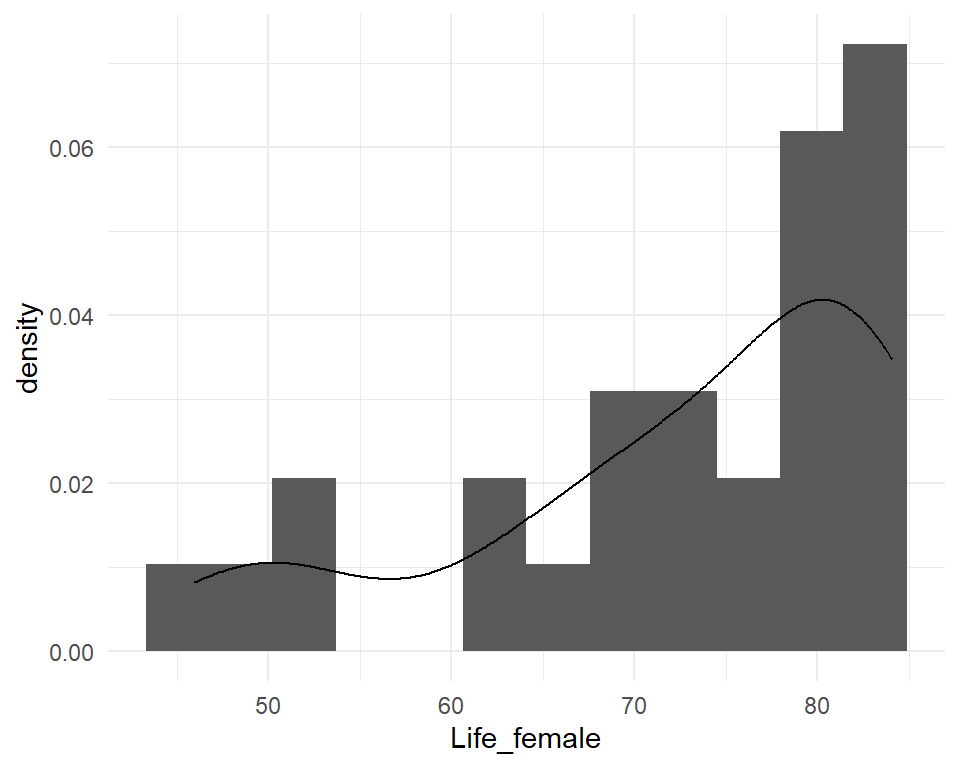
Frequency polygon & kernel density plots
Kernel density estimation (KDE)
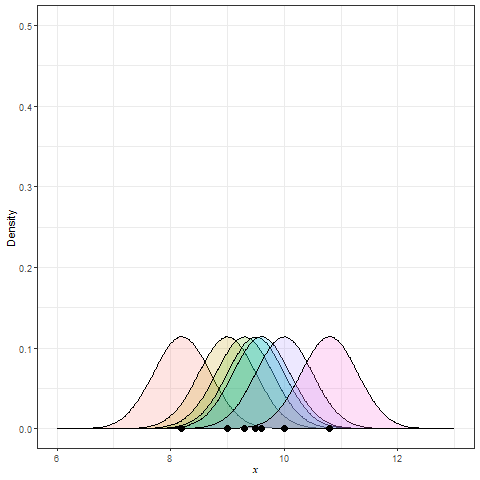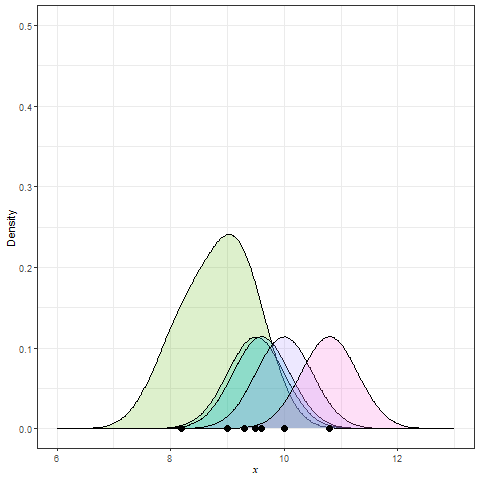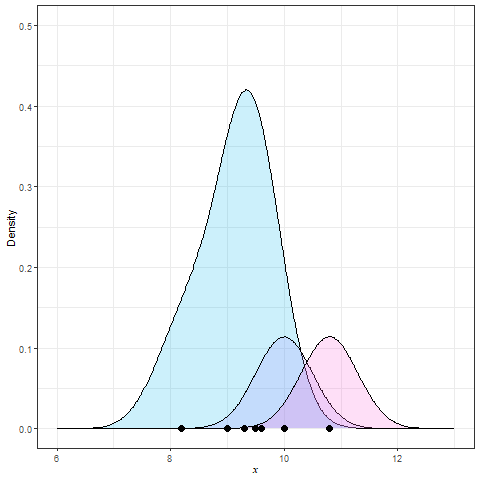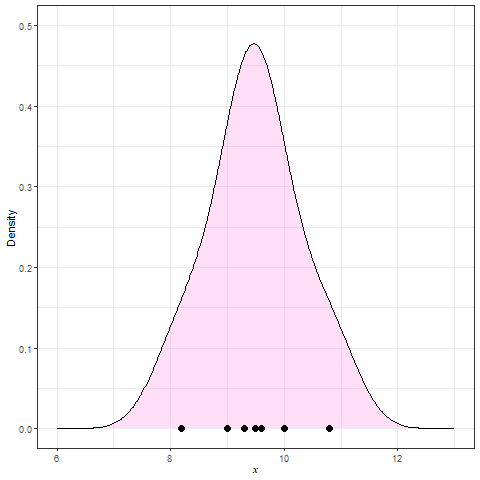
Summary statistics for EDA
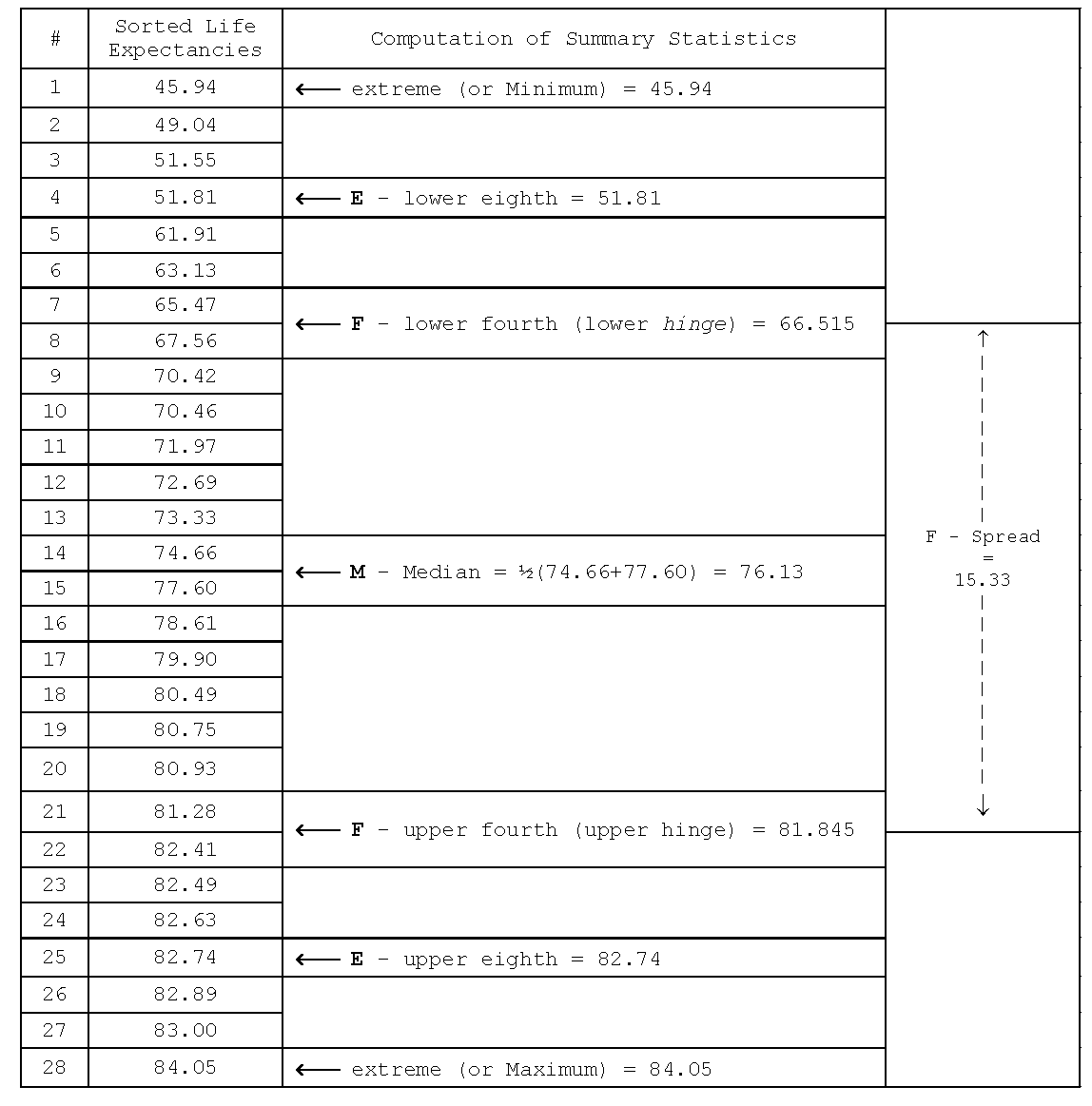
Five-number summary
Minimum, lower hinge, median, upper hinge and maximum
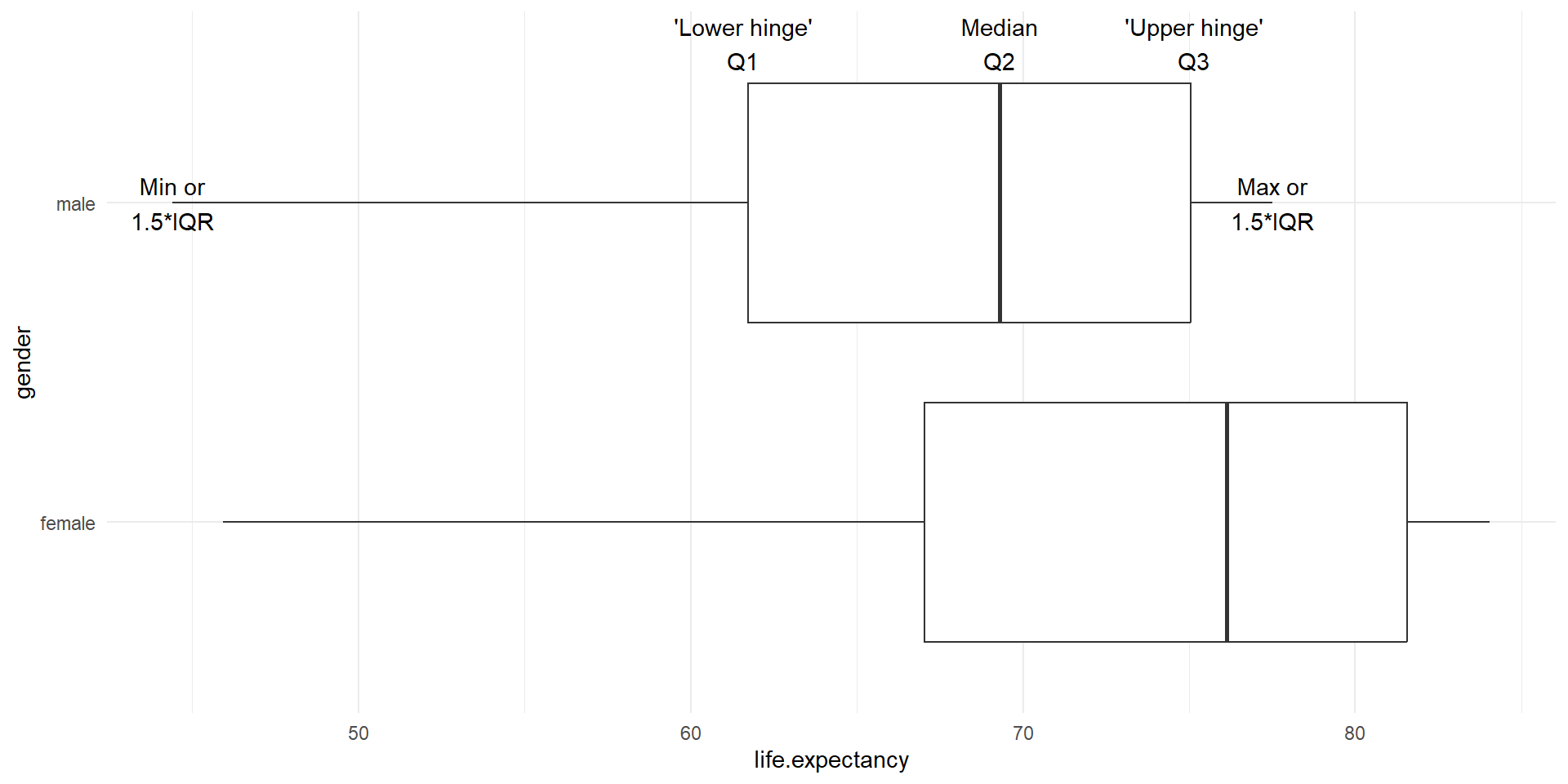
Boxplots
- Graphical display of 5-number summary
- Can show several groups of data on the same graph
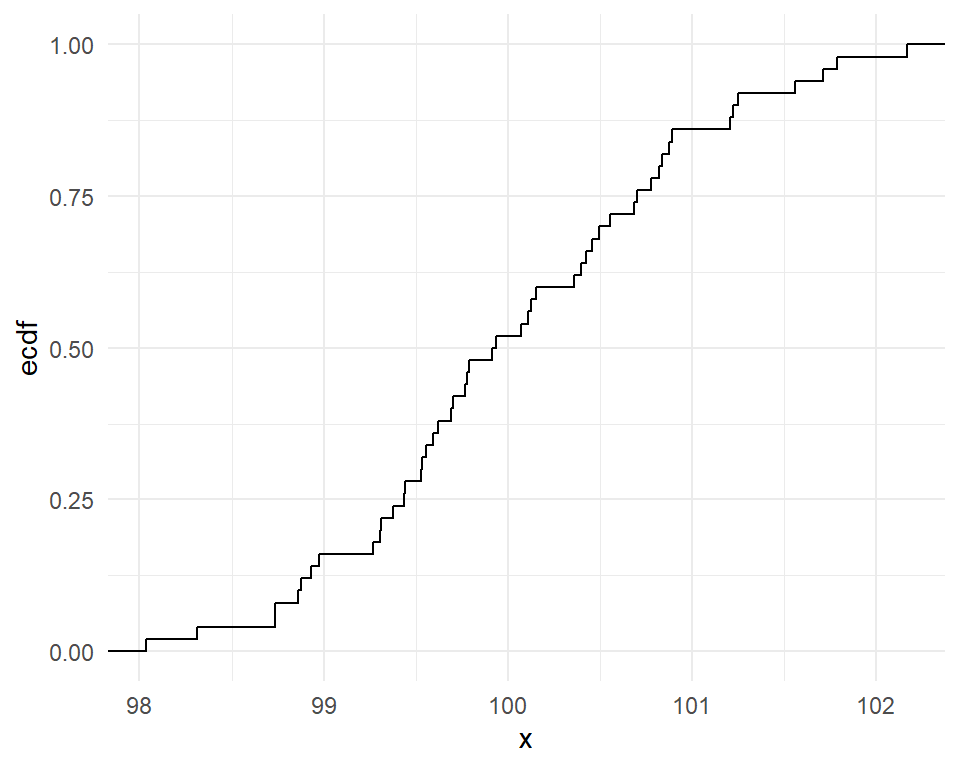
Cumulative frequency graphs
- Show the left tail area
- Useful to obtain the quantiles (deciles, percentiles, quartiles etc)
Shiny apps
Lots of examples are available
- In the study guide and workshops for this course (though not all of them are working currently)
- On the web
https://shiny.massey.ac.nz/anhsmith/demos/explore.univariate.graphs/
https://shiny.massey.ac.nz/anhsmith/demos/get.univariate.plots/
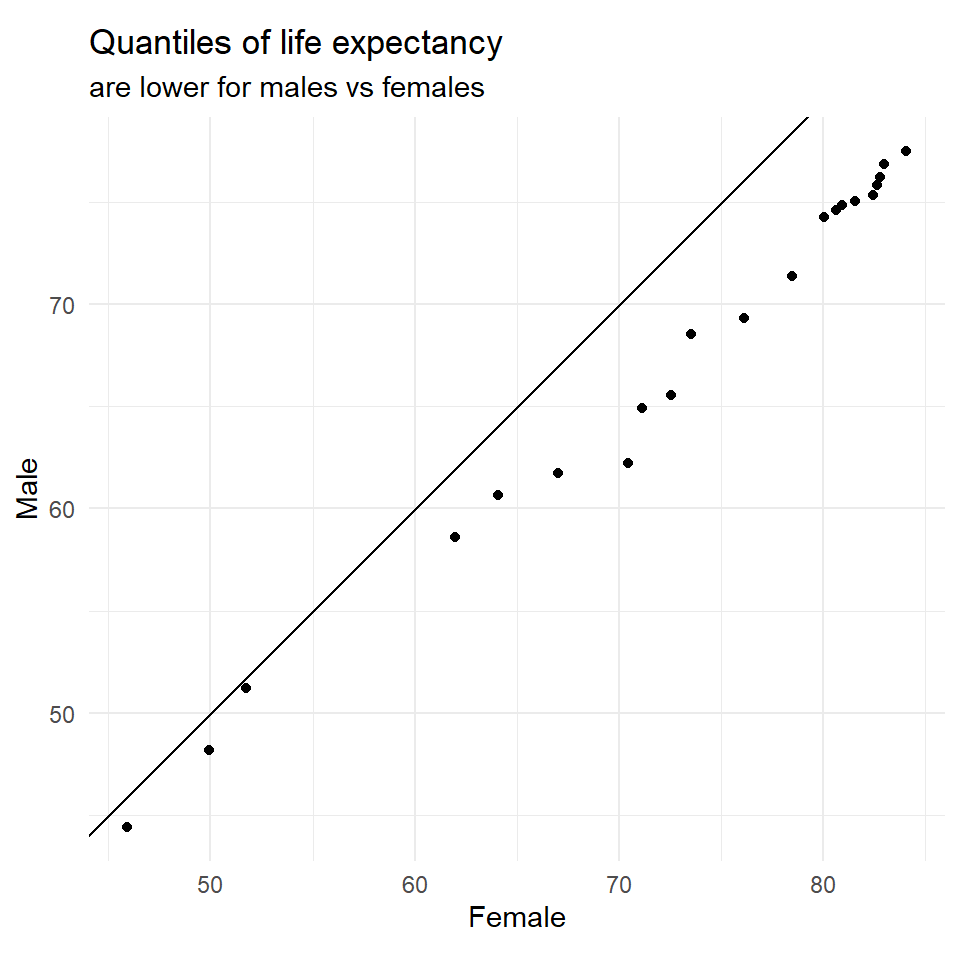
Quantile-Quantile (Q-Q) plot
Q-Q plots compare the distributions of two data sets by plotting their quantiles against each other.
vital <- read.table(
"https://www.massey.ac.nz/~anhsmith/data/vital.txt",
header=TRUE, sep=",")
quants <- seq(0, 1, 0.05)
vital |>
summarise(
Female = quantile(Life_female, quants),
Male = quantile(Life_male, quants)
) |>
ggplot() +
aes(x = Female, y = Male) +
geom_point() +
geom_abline(slope=1, intercept=0) +
coord_fixed() +
ggtitle(
"Quantiles of life expectancy",
subtitle = "are lower for males vs females"
)
Some Q-Q Plot patterns
Case a: Quantiles of Y (mean/median etc) are higher than those of X
Case b: Spread or SD of Y > spread or SD of X
Case c: X and Y follow different distributions
![]()
- R function:
qqplot().
- R function:
Bivariate relationships
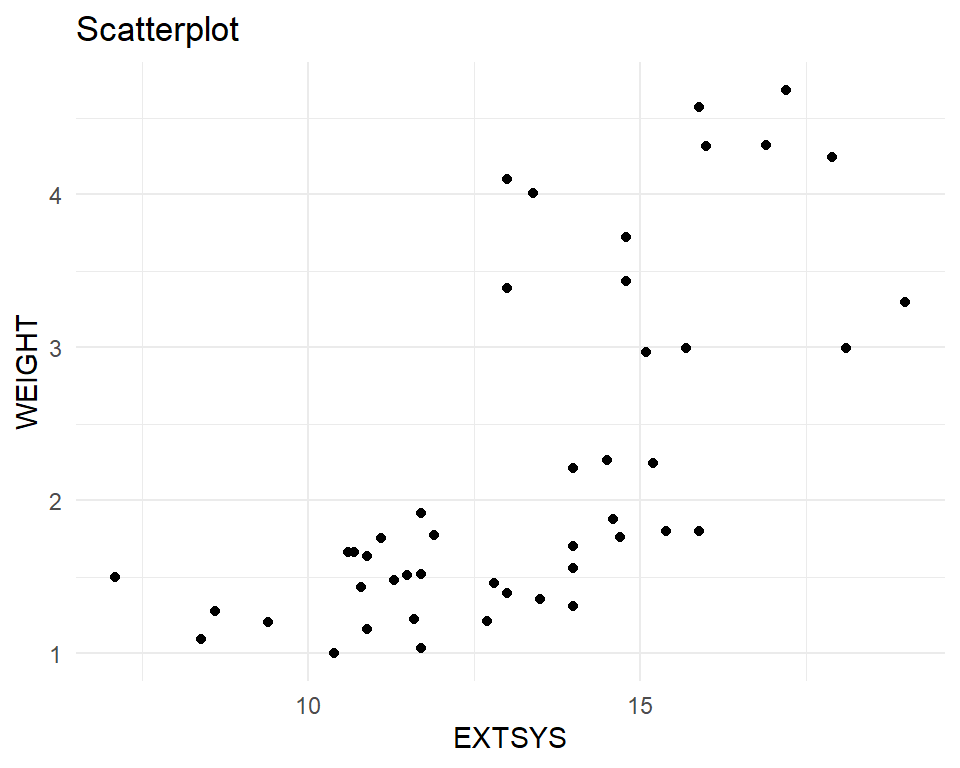
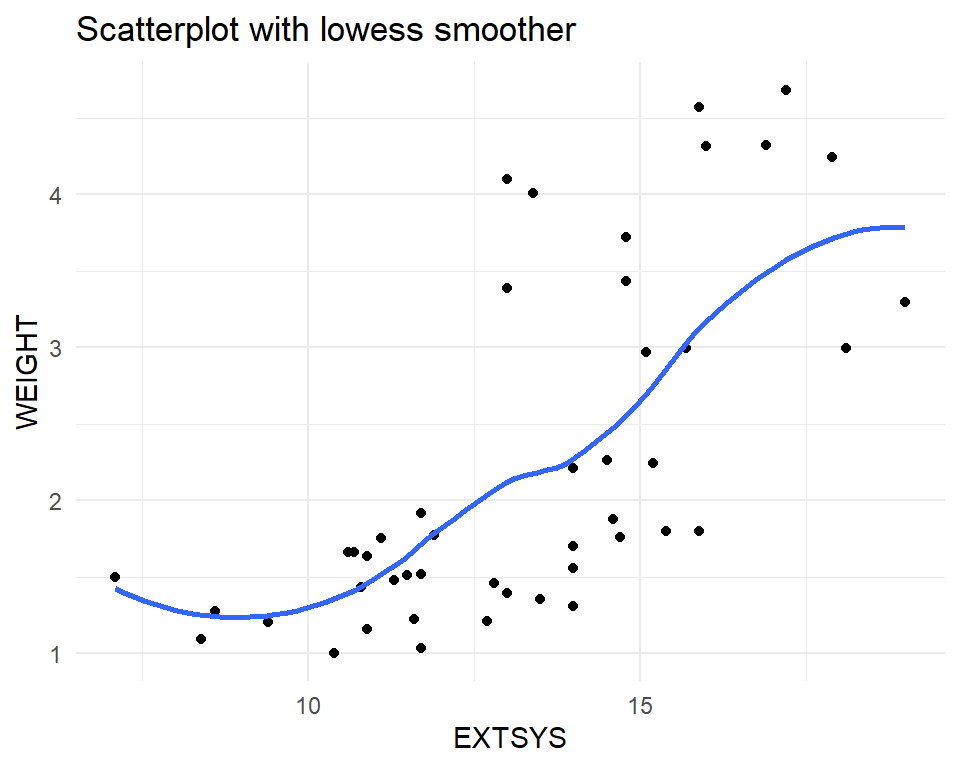
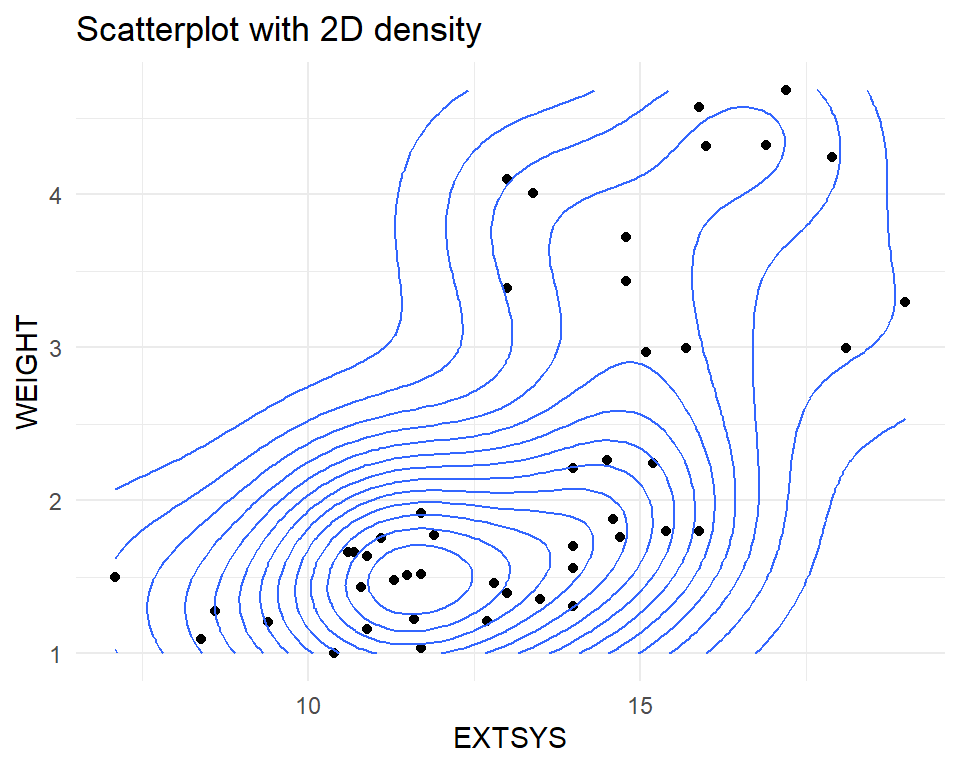
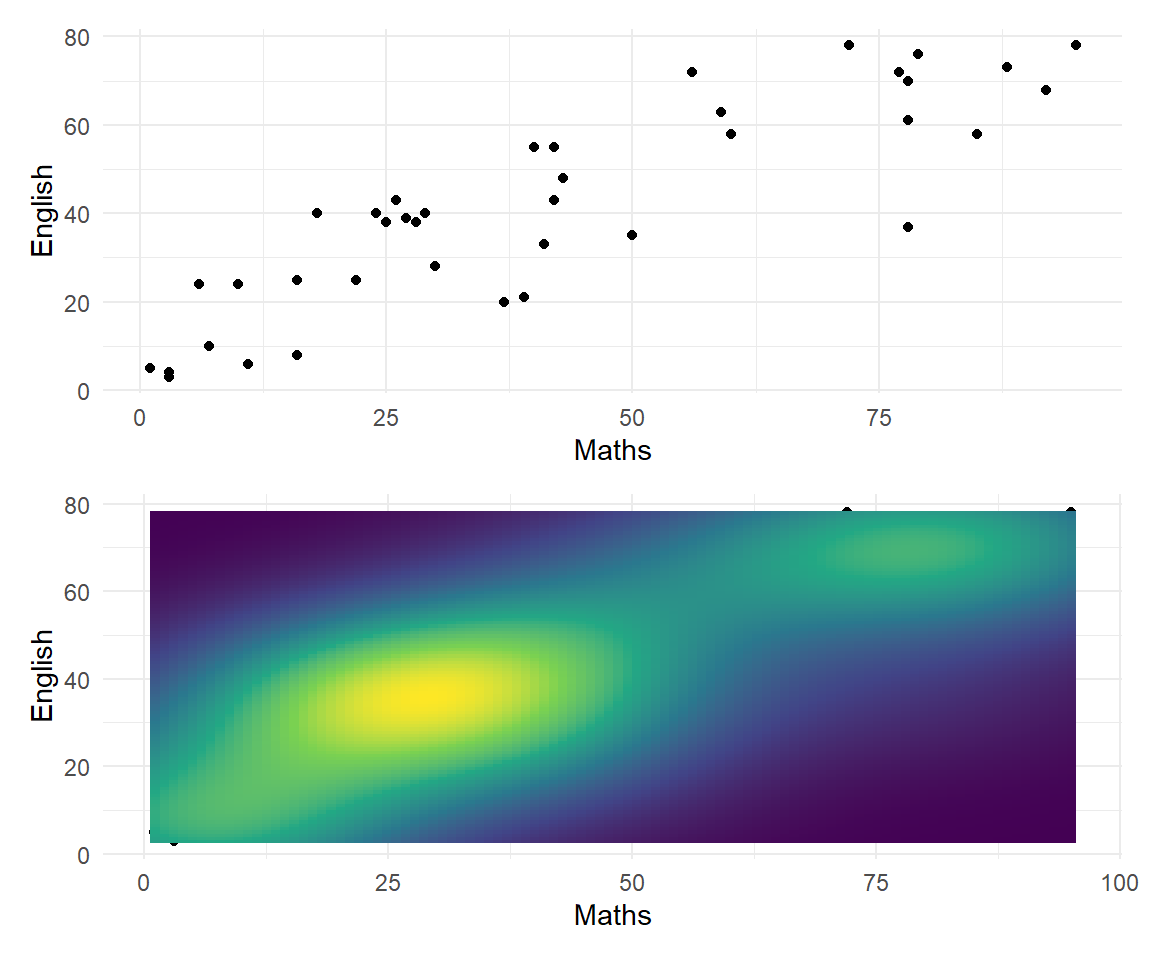
A scatter plot shows the relationship between two quantitative variables. It can highlight linear or non-linear relationships, gaps/subgroups, outliers, etc. A lowess smoother or 2D density can help show the relationship.
Bivariate relationships
A scatter plot shows the relationship between two quantitative variables. It can highlight linear or non-linear relationships, gaps/subgroups, outliers, etc. A lowess smoother or 2D density can help show the relationship.
Bivariate relationships
A scatter plot shows the relationship between two quantitative variables. It can highlight linear or non-linear relationships, gaps/subgroups, outliers, etc. A lowess smoother or 2D density can help show the relationship.
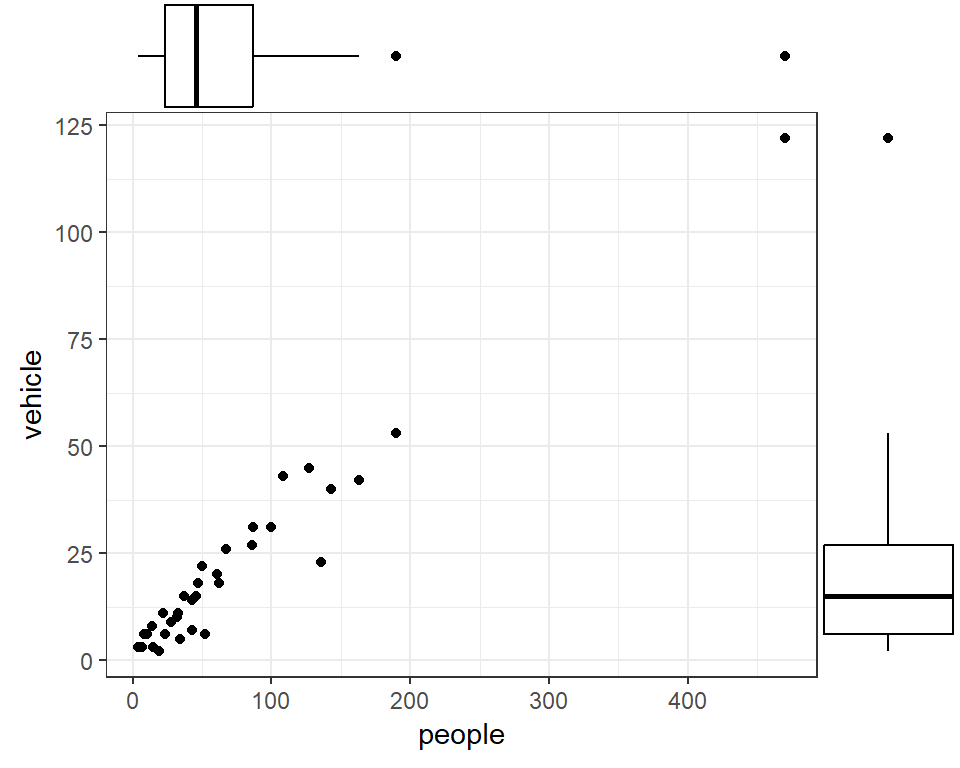
Marginal Plot
Shows both bivariate relationships and univariate (marginal) distributions
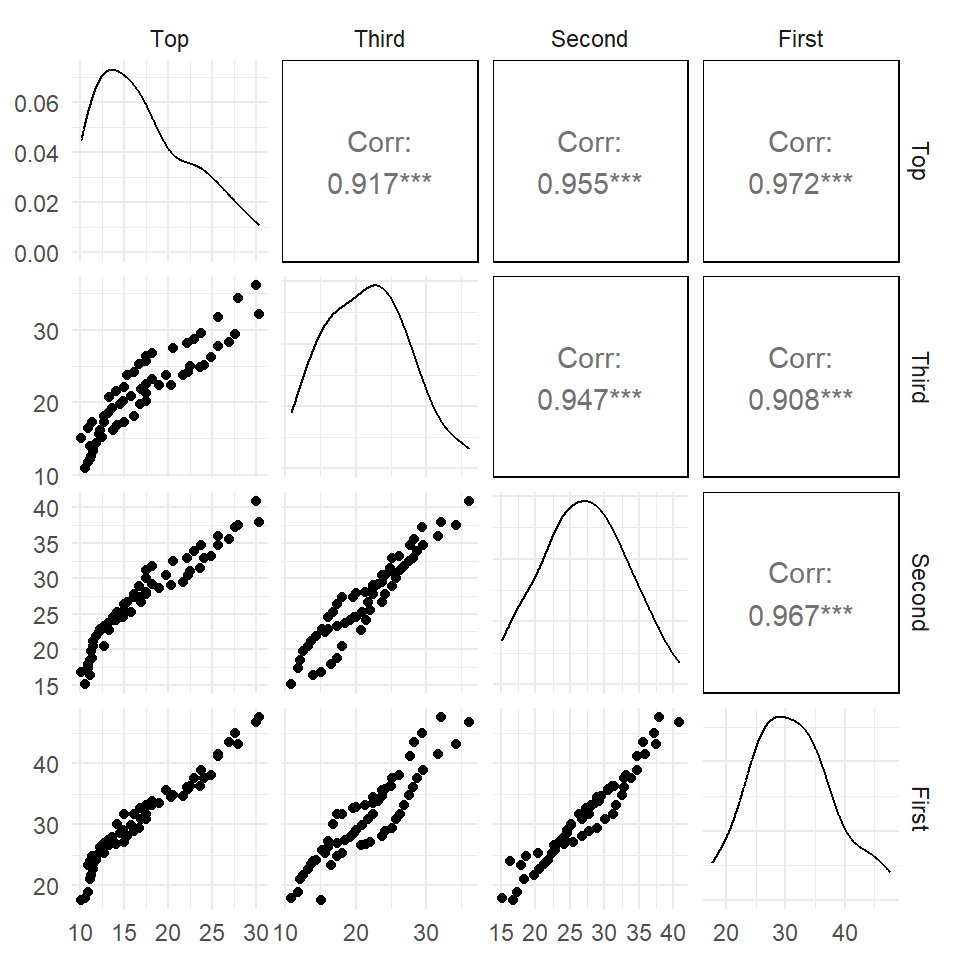
Pairs plot / scatterplot matrix
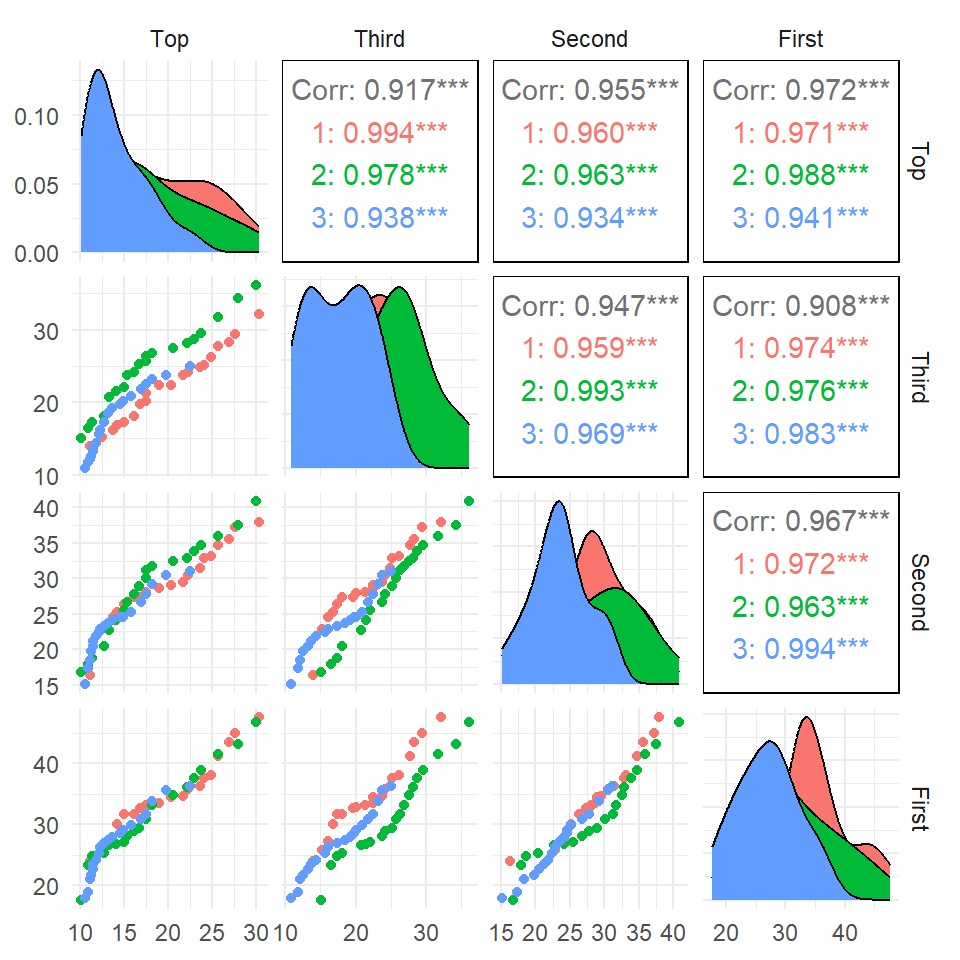
Pairs plot with a grouping variable
Correlation coefficients
The Pearson correlation coefficient measures the linear association between two variables.
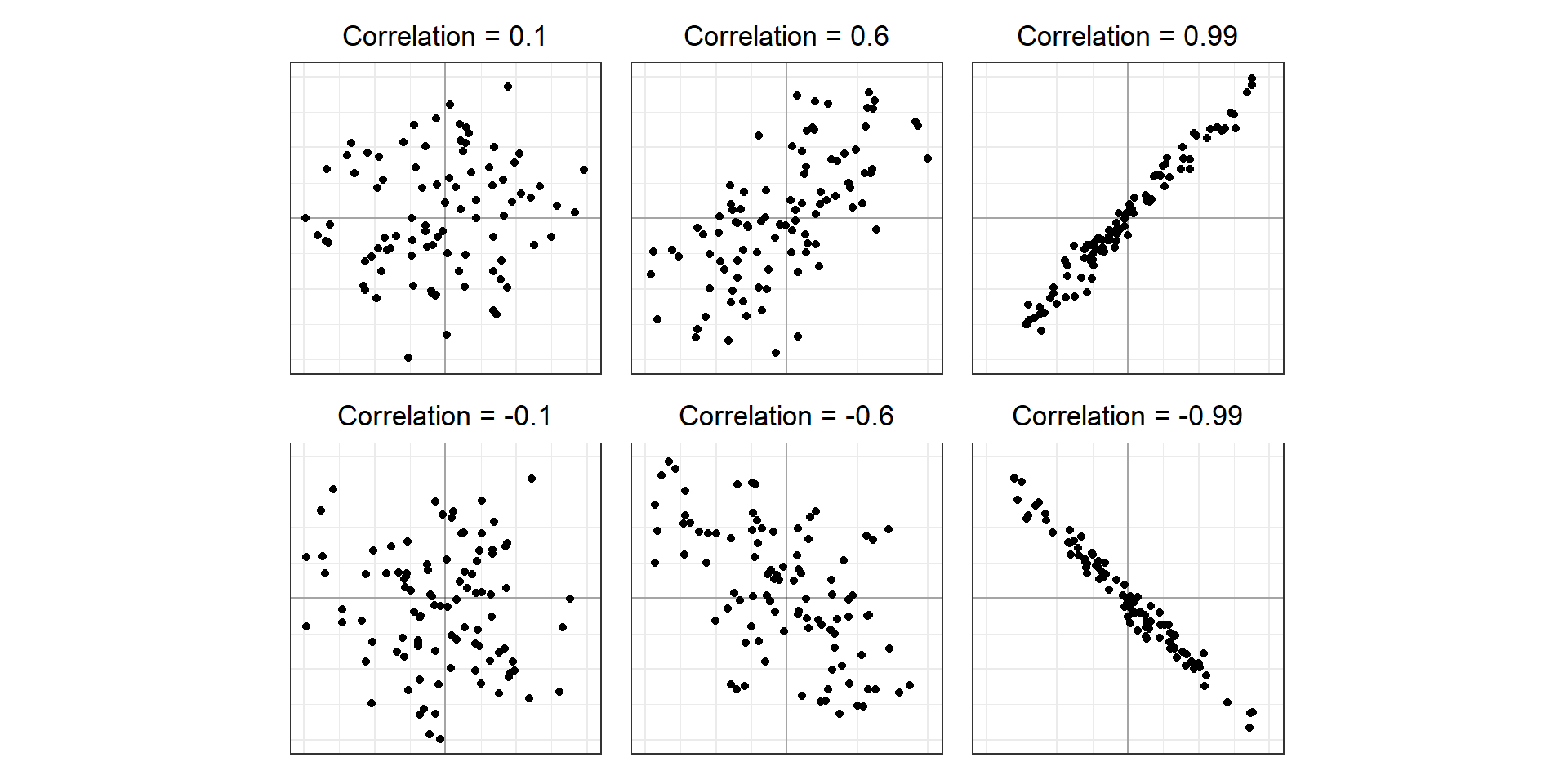
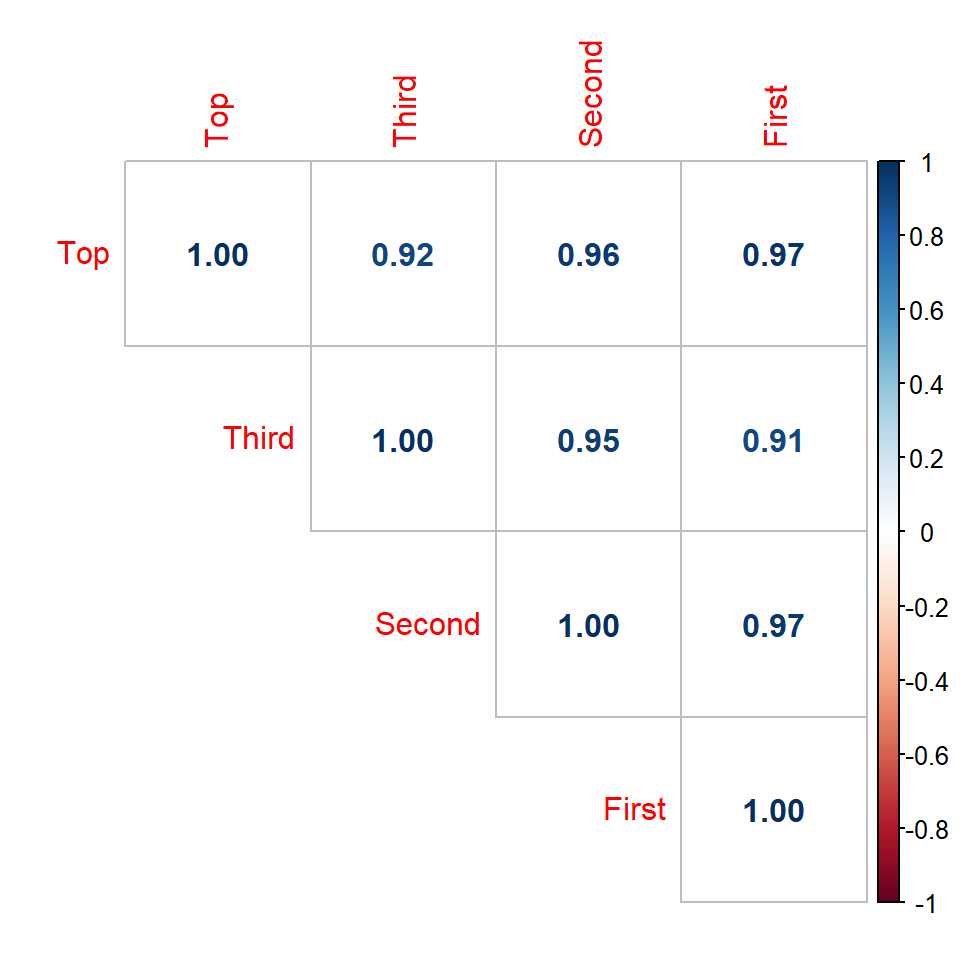
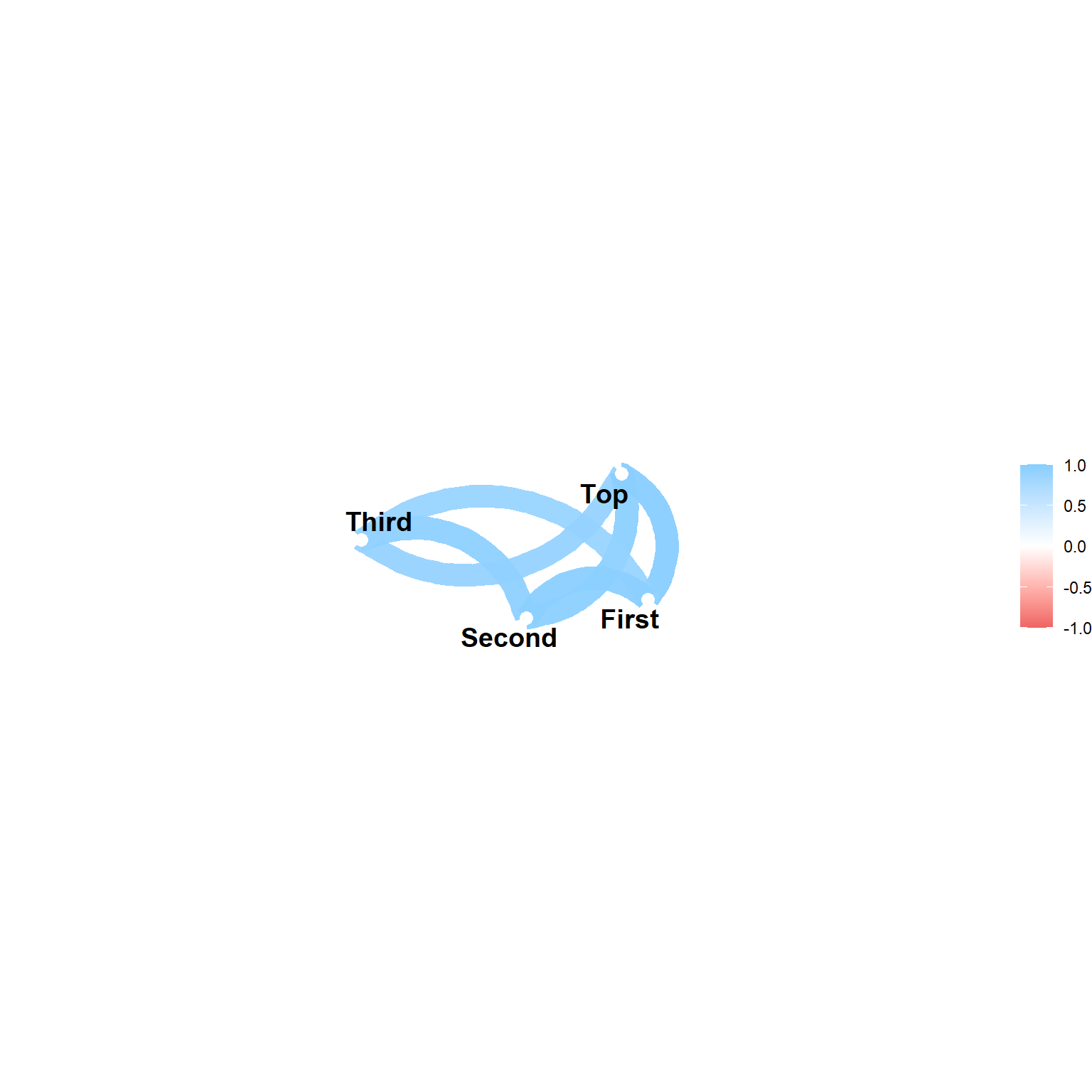
Correlation Matrix
- To show all pairwise correlation coefficients
- Useful to explore the inter-relationship between variables
Call:corr.test(x = pinetree[, -1])
Correlation matrix
Top Third Second First
Top 1.00 0.92 0.96 0.97
Third 0.92 1.00 0.95 0.91
Second 0.96 0.95 1.00 0.97
First 0.97 0.91 0.97 1.00
Sample Size
[1] 60
Probability values (Entries above the diagonal are adjusted for multiple tests.)
Top Third Second First
Top 0 0 0 0
Third 0 0 0 0
Second 0 0 0 0
First 0 0 0 0
To see confidence intervals of the correlations, print with the short=FALSE optionCorrelation Plots
Network plots
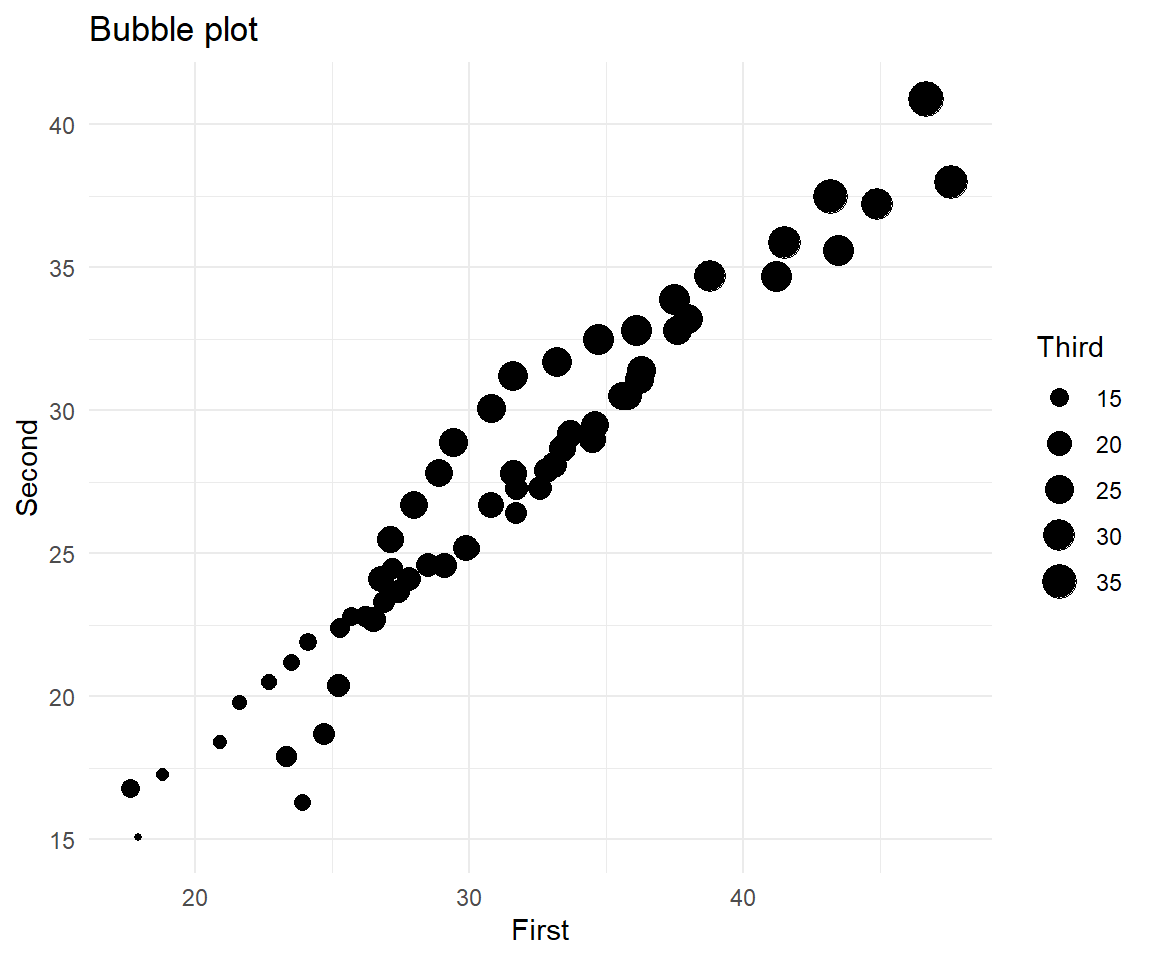
3-D Plots
A bubble plot, shows the third (fourth) variable as point size (colour).
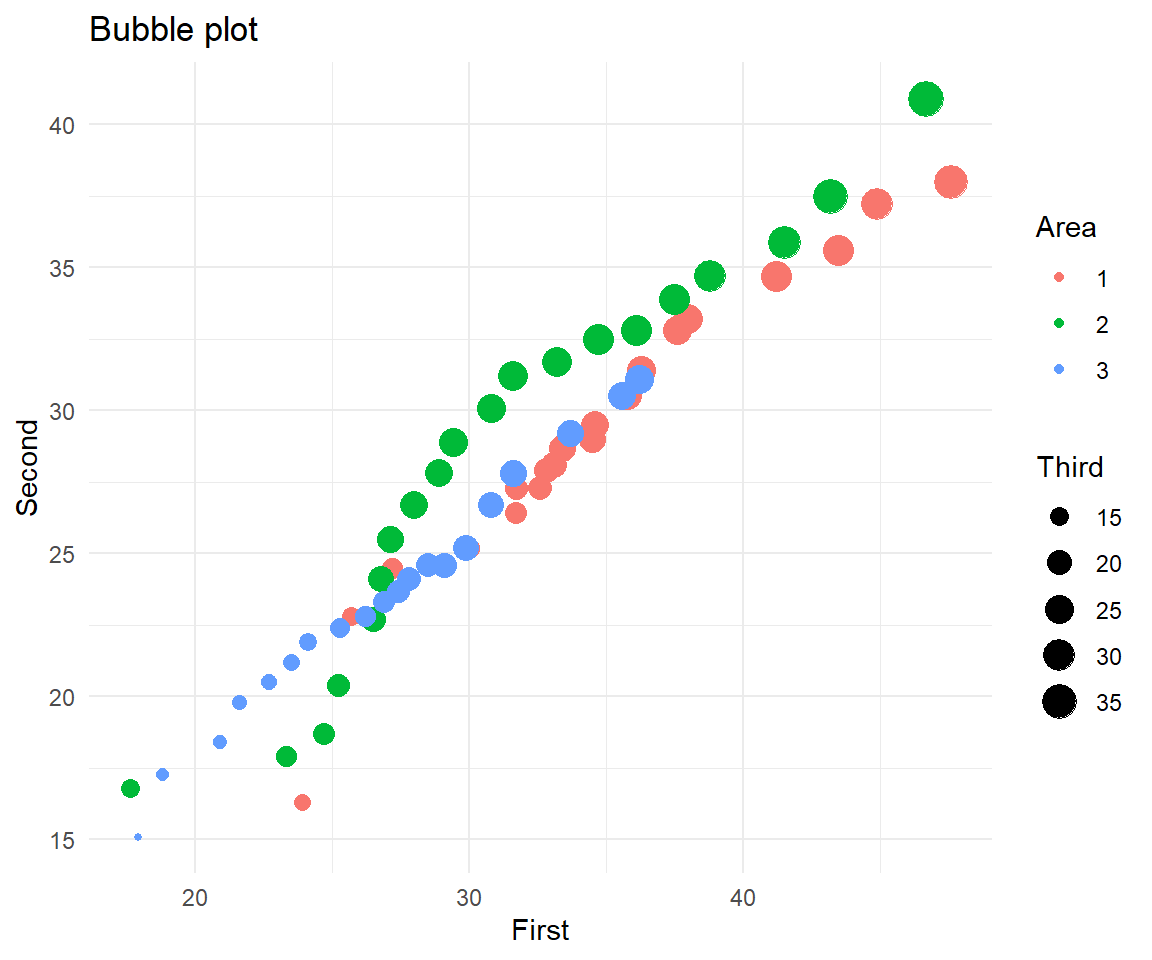
3-D Plots
A bubble plot, shows the third (fourth) variable as point size (colour).
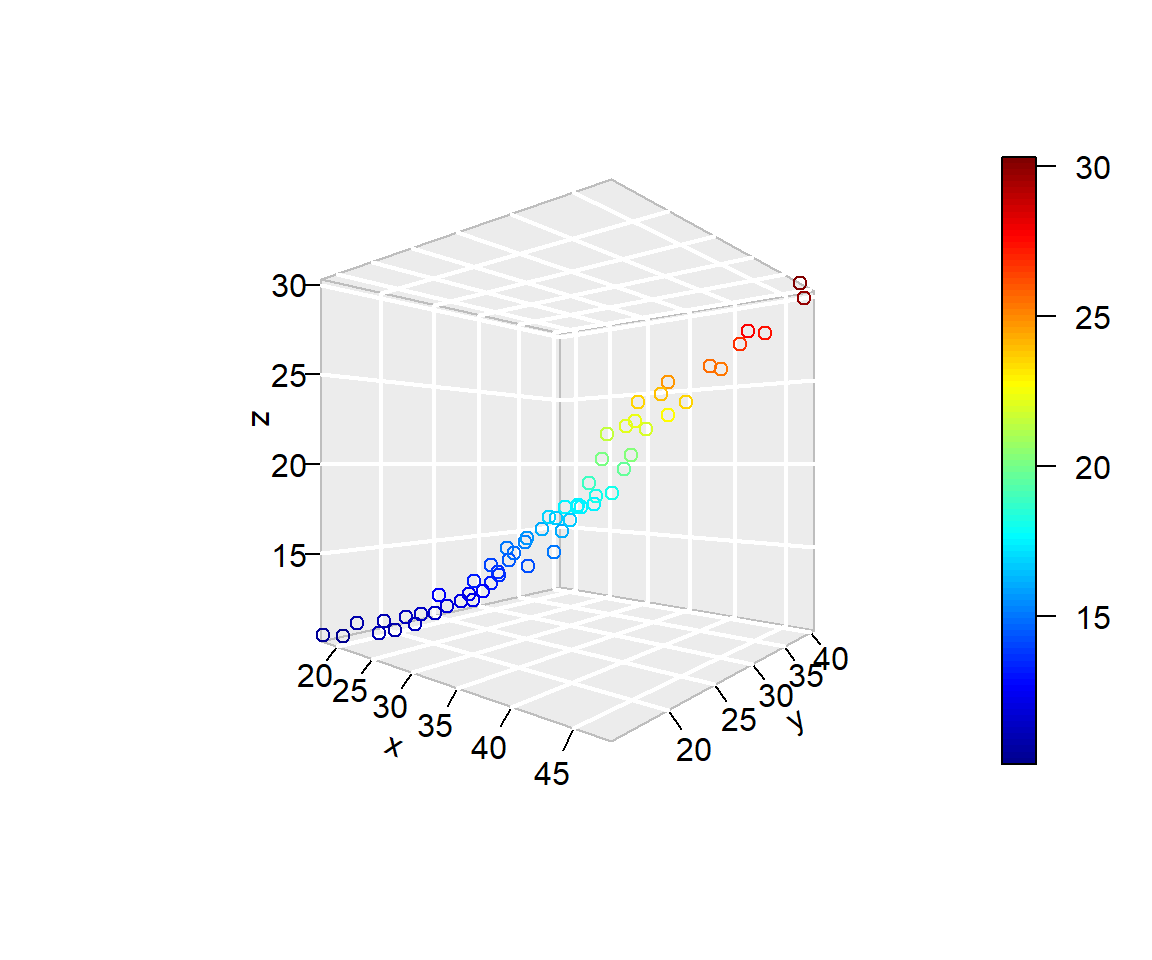
3-D plots are far more useful if you can rotate them
Package plot3D
3-D plots are far more useful if you can rotate them
Package plotly
Contour plots
3D plots are difficult to interpret than 2D plots in general
Contour plots are another way of looking three variables in two dimensions
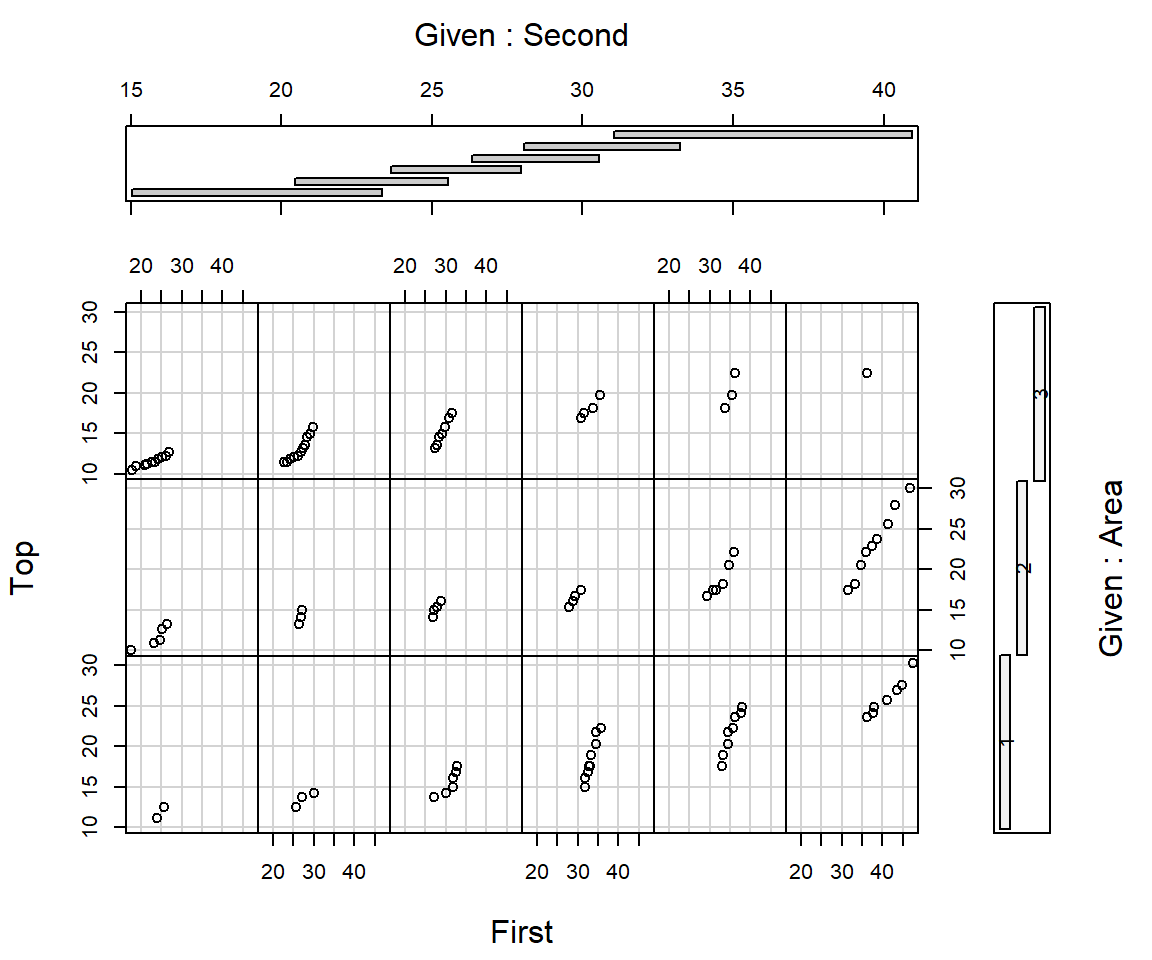
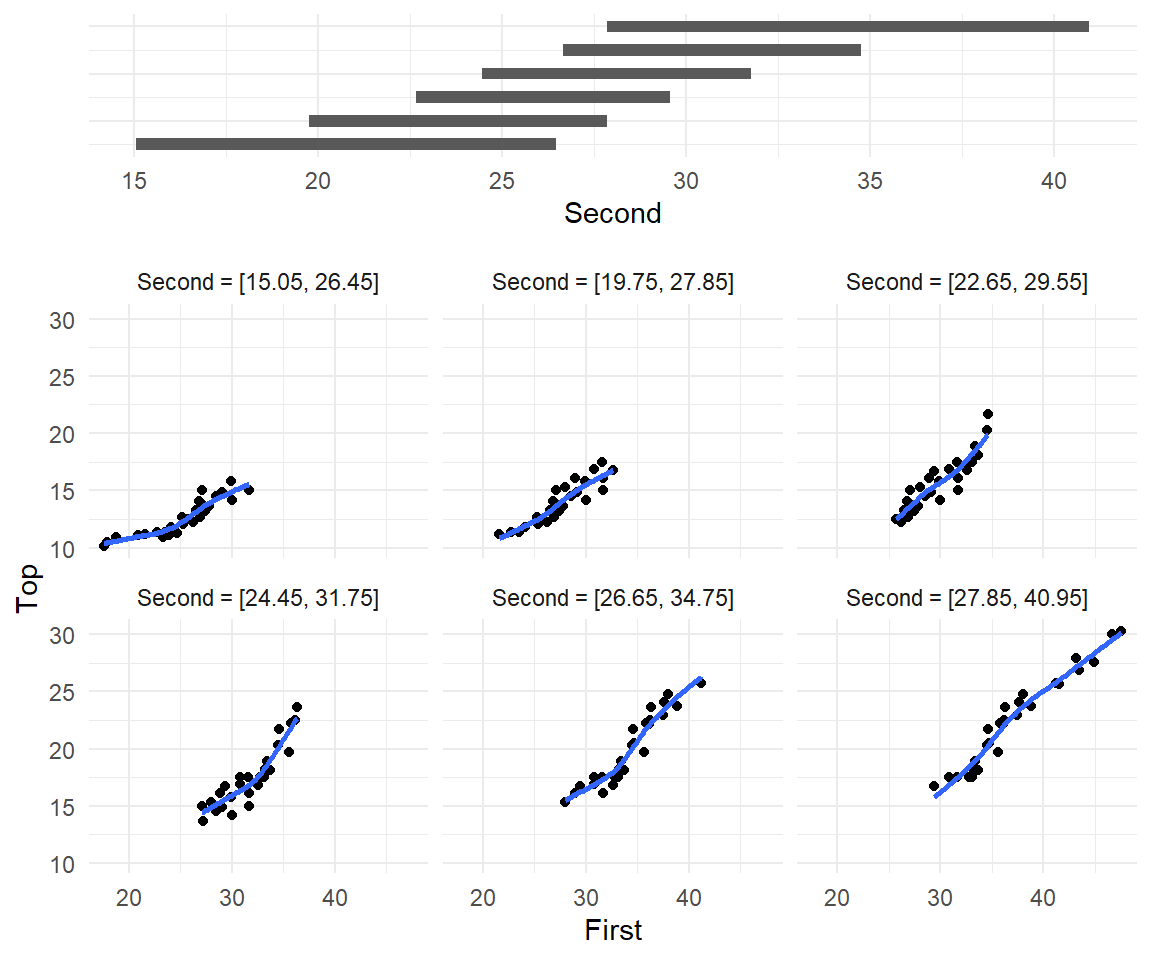
Conditioning plots
Conditioning Plots (Coplots) show two variables at different ranges of third variable
Conditioning plots
Conditioning Plots (Coplots) show two variables at different ranges of third variable
More R graphs
Build plots in a single layout (R packages patchwork or gridExtra)
Learning EDA
The best way to learn EDA is to try many approaches and find which are informative and which are not.
Chatfield (1995) on tackling statistical problems:
- Do not attempt to analyse the data until you understand what is being measured and why. Find out whether there is prior information such as are there any likely effects.
- Find out how the data were collected.
- Look at the structure of the data.
- The data then need to be carefully examined in an exploratory way before attempting a more sophisticated analysis.
- Use common sense, and be honest!
Summary
Size
- For small datasets, we cannot be too confident in any patterns we see. More likely for patterns to occur ‘by chance’.
- Some displays are more affected by sample size than others
Shape
- In can be interesting to display the overall shape of distribution.
- Are there gaps and/or many peaks (modes)?
- Is the distribution
symmetrical? Is the distributionnormal?
Outliers
- Boxplots & scatterplots can reveal outliers
- More influential than points in the middle
Graphs should be simple and informative; certainly not misleading!